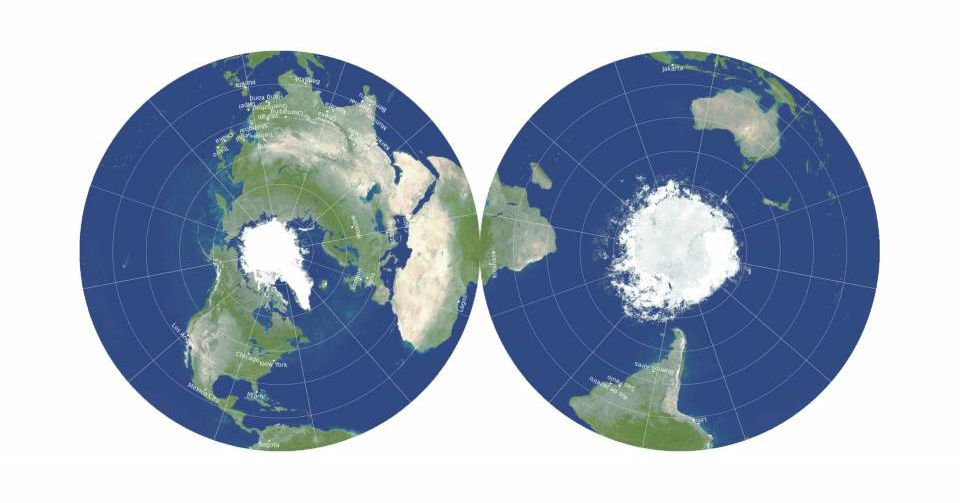
A trio of scientists have devised a new way to try to represent our spherical planet as a flat picture with a new class of projection that involves printing the map as a double-sided circle, Phys.org reports. The Double-Sided Gott projections involve splitting a globe in two and printing the separate hemispheres on separate sides. The paper is the work of J. Richard Gott, Robert Vanderbei, and David Goldberg from Princeton and Drexel universities.
While 3D globes are the most accurate way of representing the layout of the Earth’s surface, it’s much more convenient to refer to a 2D representation. There are a variety of ways of converting this 3D shape into 2D, which are referred to as map projections, but none of them are perfect.
The most famous projection is probably the Mercator projection (which is used by Google Maps for local area maps), but it gets really distorted near the North and South poles. The Winkel Tripel is another option, and it’s the one used by National Geographic for its world maps, but it still splits the Pacific Ocean in two.
In 2007, Goldberg and Gott devised a system for scoring the accuracy of flat maps, where the closer a score is to zero, the more accurate it is. A globe, for instance, would get a perfect zero. By their calculations, the Mercator projection scores 8.296 and Winkel Tripel does better at 4.563. Their own azimuthal equidistant double-sided projection, meanwhile, scores 0.881. “We believe it is the most accurate flat map of Earth yet,” the trio write.
It might technically be flat, but having a map printed on two sides of a piece of paper introduces obvious limitations. The scientists admit that “our double-sided flat map is actually more like the globe of the Earth than the other flat maps” because you can’t see both sides at once. Instead, they see it as the kind of map that might be included as an extra sheet in a magazine, or printed on cardboard or plastic and stored in boxes.
For more about the problems with 2D projections, check out this video from Vox below.
